
La Proyección Ortogonal, es uno de los conceptos más empleados no solo en las matemáticas, sino también en la física y en dibujo técnico; En bachillerato es el nivel donde se empieza a estudiar este objetivo y dependiendo de la carrera, que desees estudiar a nivel universitario, se siguen haciendo aplicaciones con proyecciones. Si estudias diseño en 2D y 3D, éste termino está implícito en determinadas herramientas y aplicaciones.
Por lo que te invito a que descubras leyendo en este post, ¿Qué es? y ¿Para qué sirve? y otros detalles relacionados con esta temática como:
- Sistema de coordenadas.
- Función Afín.
Proyección Ortogonal ¿Qué es?
Las proyecciones ortogonales son mayormente estudiadas en el área de la geometría y las matemáticas aplicadas; Se refieren a aquella cuyas rectas proyectantes auxiliares son perpendiculares al plano de proyección (o a la recta de proyección), estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.
El concepto de proyección ortogonal se generaliza a espacios euclidianos de dimensión arbitraria, inclusive de dimensión infinita. Esta generalización tiene un papel importante en muchas ramas de matemática y física.
Hallar la proyección ortogonal de puntos y segmentos sobre una recta
Esta es una se las preguntas más comunes al momento de estudiar este eje temático. Por lo que, en el plano, la proyección ortogonal tanto para un punto y segmentos sobre una recta, se realiza de la misma forma, se trazan líneas proyectantes auxiliares las cuáles son perpendiculares a la recta de proyección que en este caso se llamará “ L”.
A continuación los casos más comunes sobre proyección ortogonal de un punto y un segmento:
A.- Proyección ortogonal de un punto
Ejemplo:
Caso General: La proyección ortogonal de un punto P en una recta L es otro punto A que se obtiene trazando una línea auxiliar perpendicular a L desde el punto A tal que esta línea pase por P. Lógicamente, si el punto P pertenece a la recta L, coinciden: P = A .
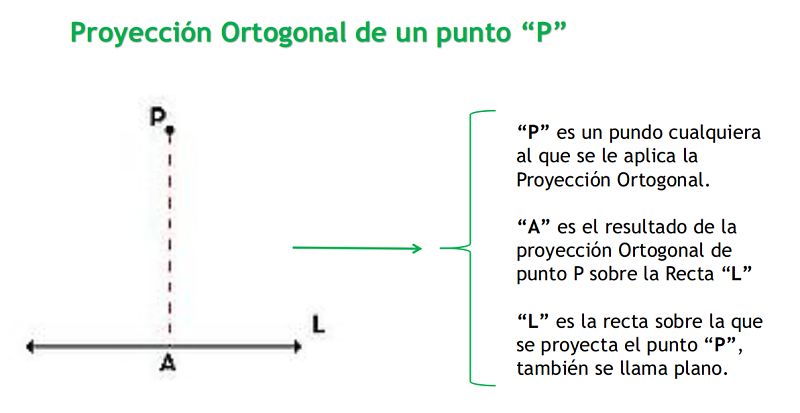
B.- Proyección ortogonal de un segmento
Ejemplo:
4 Casos generales:
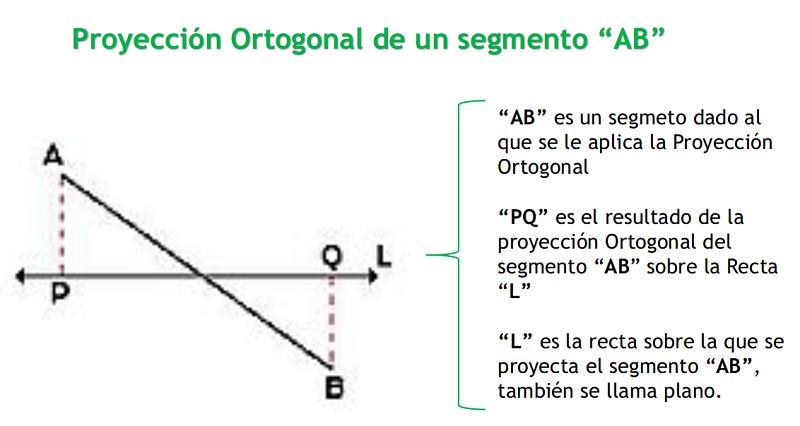
1.- Si el segmento dado AB no es paralelo a la recta L, la proyección ortogonal es un segmento PQ que se obtiene trazando líneas perpendiculares a X desde los puntos extremos de AB. La magnitud de la proyección siempre es menor que la del segmento dado.
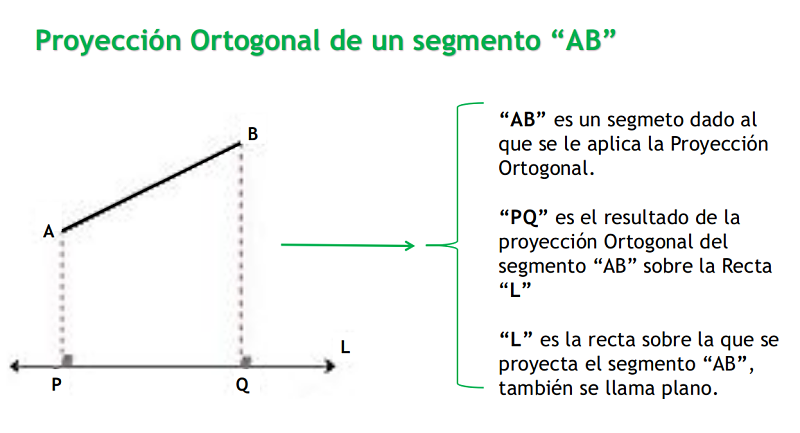
2.- Si el segmento PQ y la recta X son paralelos, la proyección ortogonal será: AB = PQ, que se obtiene de forma análoga.
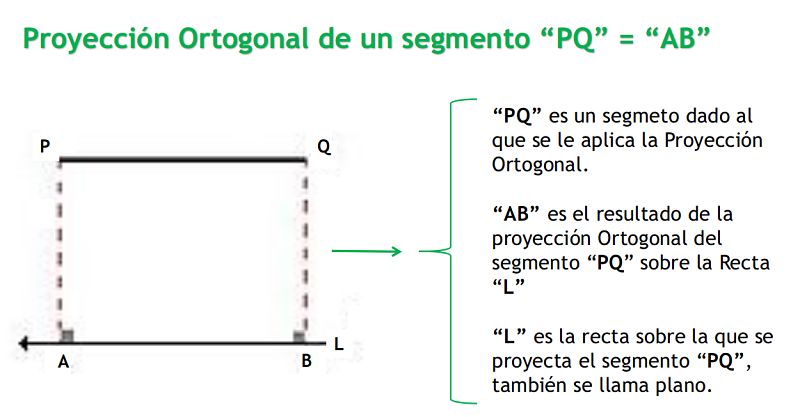
3.- Si el segmento AB tiene un punto común con la recta L, la proyección ortogonal se obtiene de modo similar.
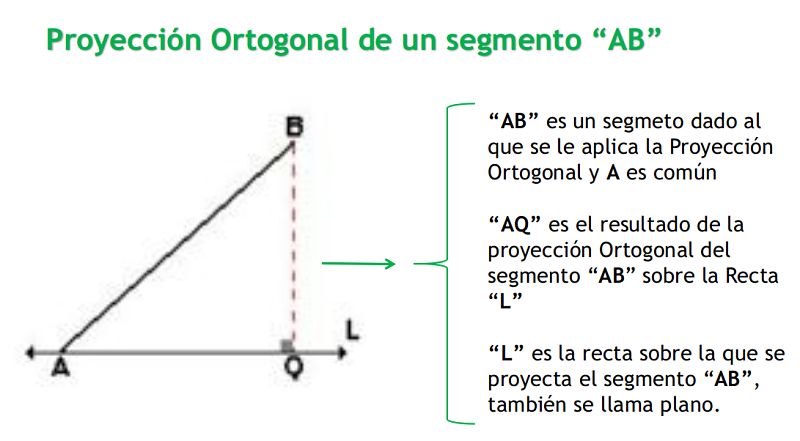
4.- Si el segmento AB corta a la recta L, la proyección ortogonal se obtiene de forma análoga.
¿Para qué sirve la proyección Ortogonal?
Son uno de los recursos matemáticos para obtener un punto o un segmento de una recta con respecto a un plano u otra recta y en esta última hallar de forma análoga su equivalente con la ayuda de la líneas auxiliares, tal como se apreciaron en los 4 casos generales arriba.
Tenemos más artículos que te pueden interesar:
- Formación de tejidos y órganos: 2 aspectos fundamentales en la Bioingeniería
- Historia natural de la Diabetes Mellitus, 7 preguntas más frecuentes
- La Regeneración: Mitología o realidad
Sistema de coordenadas rectangulares
El sistema de coordenadas rectangulares es también conocido como sistema cartesiano, se emplean como un recurso valioso, para la representación gráfica de una relación matemática o del movimiento o posición en física. Este sistema se caracteriza por tener referencia ejes ortogonales y perpendiculares entre sí que se interceptan en el punto llamado origen.
El plano cartesiano se utiliza para asignarle una ubicación a cualquier punto en el plano; por lo que, un sistema de coordenadas rectangulares es un sistema bidimensional, el cuál se compone por dos ejes (Abscisas = eje de las “X”), (Ordenadas = Eje de las “Y”).
Por otro lado, es de gran interés saber que al tener los dos ejes cartesianos, dividen al plano en cuatro regiones o zonas, que hoy conocemos como cuadrantes:
- Cuadrante “I”: Está ubicada en la zona superior a la derecha.
- Cuadrante «II»: Zona superior izquierda.
- Cuadrante «III»: Zona inferior izquierda.
- Cuadrante «IV»: Zona inferior derecha.

Representar un punto en un sistema de coordenadas rectangulares, mediante una gráfica
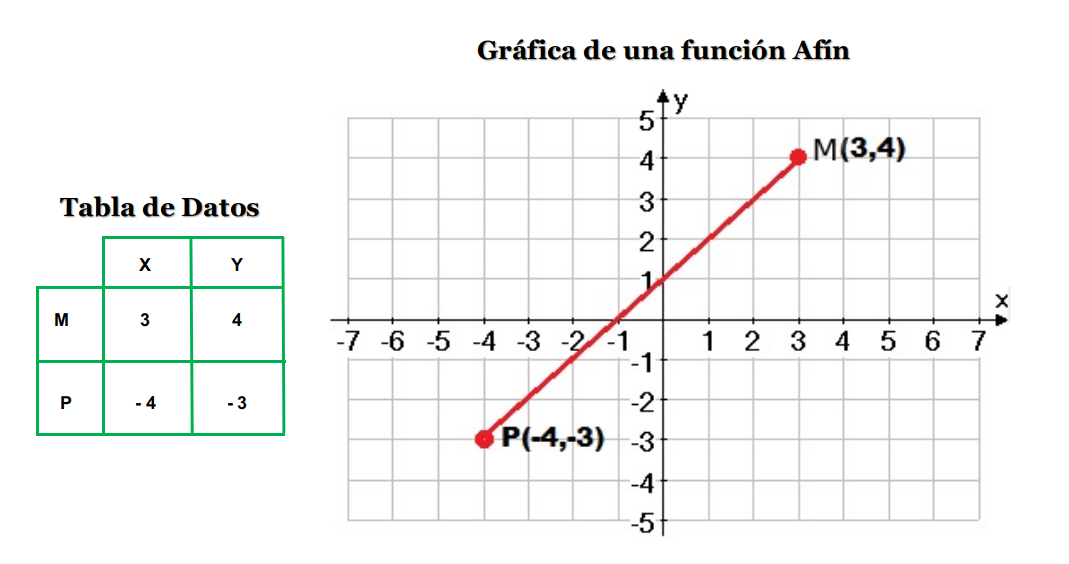
A partir de una tabla con dos puntos M (3, 4) y P (-4, -3), se procede a ubicar las coordenadas rectangulares con un sistema de coordenadas cartesiano tal como se aprecia en en la siguiente imagen abajo.
Función Afín
Una función afín es una función que, en cualquier valor x definido en ℝ (la escala de los números reales), asocia el número ax + b, siendo «a» y «b» números relativos.
- Representamos esta función mediante la ecuación siguiente: f(x): ax + b
- El número «b» debe ser diferente a 0. ¿Por qué? Porque si b = 0, entonces tenemos que f(x) = ax y entonces hablamos de una función afín lineal.
- Si «a» es igual a cero, entonces decimos que la función f(x) = b es constante (y afín); de hecho, todos los puntos de la misma línea tienen el mismo eje de ordenadas (b) y la curva será paralela al eje de abscisas.
- Por lo que en resumen, una función afín es un conjunto de valores que resuelve la ecuación y = ax + b, en el intervalo dado, y cuya representación gráfica tomará la forma de una recta oblicua, creciente o decreciente.
Si quieres leer más sobre otros temas de interés:
Albert Einstein científico: Teoría de la relatividad especial, 3 Postulados
¿Sabías que la Brújula apunta al norte, porque su imán es atraído por la tierra?
¡Eureka! La luz es una Onda Electromagnética desarrollado por 2 Científicos
Identificar una Función Afín
Una función afín, viene definida por una relación o correspondencia entre dos variables o conjunto de variables X e Y. siendo esta relación resuelta por una ecuación que teóricamente se define como:
y = +/- m(x) +/- n
Es decir, la ecuación admite signos positivos y negativos, tanto del coeficiente de variable “m” como del termino independiente “n”.
En efecto, de esta relación matemática se pueden obtener datos y llevarlos a una representación gráfica que puede ser creciente o decreciente.
En resumen existen dos formas probables de identificar una función afín:
A.- Que la ecuación corresponda a una similar a esta f(x): ax + b
En la que a y b son números que pueden ser de signo positivo o negativo.
B.- Dado algunos casos en los que no se tiene la ecuación, pero si la gráfica; esta debe ser una recta lineal ya sea Inclinada u oblicua, horizontal o vertical respectivamente.
Representar gráficamente funciones afines en el plano
A continuación con dos ejemplos podemos entender mejor como se representan gráficamente las funciones afín.
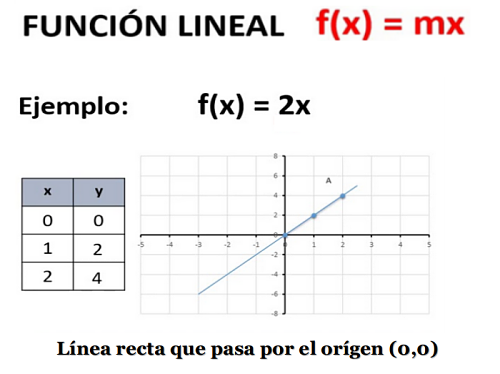
Caso 1
F(x) = 2(x)
Caso 2
F(x) = 2(x) + 2

